• As the documentation says. The LIMIT clause can be used to constrain the number of rows returned by the SELECT statement. LIMIT takes one or two numeric arguments, which must both be nonnegative integer constants (except when using prepared statements).
• Unit 1: Limits Unit 1 Quiz: September 9 Unit 1 Problem Set Due: September 19 Unit 1 Test: September 23.
• 1 Limits and Continuity We begin with a review of the concepts of limits and continuity for real-valued functions of one variable. Recall that the deflnition of the limit of such functions is as follows. Rand let a 2 R: Then limx!a f(x) = L means that for each † 0 there is.

• 1 Limits & Continuityap Calculus Calculator
• 1 Limits & Continuityap Calculus Ab
• 1 Limits & Continuityap Calculus 14th Edition

OSHA recognizes that many of its permissible exposure limits (PELs) are outdated and inadequate for ensuring protection of worker health. Most of OSHA’s PELs were issued shortly after adoption of the Occupational Safety and Health (OSH) Act in 1970, and have not been updated since that time. Learn more about how the Ohio MMCP program defines purchase and supply limits for medical marijuana, including whole day units and 90-day supplies.

Approaching ...

Sometimes we can't work something out directly ... but we can see what it should be as we get closer and closer!

Example:

(x² − 1)(x − 1)

Let's work it out for x=1:

(1² − 1)(1 − 1) = (1 − 1)(1 − 1) = 00

Now 0/0 is a difficulty! We don't really know the value of 0/0 (it is 'indeterminate'), so we need another way of answering this.

So instead of trying to work it out for x=1 let's try approaching it closer and closer:

Example Continued:

x	(x2 − 1)(x − 1)
0.5	1.50000
0.9	1.90000
0.99	1.99000
0.999	1.99900
0.9999	1.99990
0.99999	1.99999
...	...

Now we see that as x gets close to 1, then (x²−1)(x−1) gets close to 2

We are now faced with an interesting situation:

• When x=1 we don't know the answer (it is indeterminate)
• But we can see that it is going to be 2

We want to give the answer '2' but can't, so instead mathematicians say exactly what is going on by using the special word 'limit'.

The limit of (x²−1)(x−1) as x approaches 1 is 2

And it is written in symbols as:

limx→1x²−1x−1 = 2

1 x^2~−1/x−1 = 2 -->

So it is a special way of saying, 'ignoring what happens when we get there, but as we get closer and closer the answer gets closer and closer to 2'

As a graph it looks like this: So, in truth, we cannot say what the value at x=1 is. But we can say that as we approach 1, the limit is 2.

Test Both Sides!

It is like running up a hill and then finding the path is magically 'not there'...

... but if we only check one side, who knows what happens?

So we need to test it from both directions to be sure where it 'should be'!

Example Continued

So, let's try from the other side:

x	(x2 − 1)(x − 1)
1.5	2.50000
1.1	2.10000
1.01	2.01000
1.001	2.00100
1.0001	2.00010
1.00001	2.00001
...	...

Also heading for 2, so that's OK

When it is different from different sides

How about a function f(x) with a 'break' in it like this:

The limit does not exist at 'a'

We can't say what the value at 'a' is, because there are two competing answers:

• 3.8 from the left, and
• 1.3 from the right

But we can use the special '−' or '+' signs (as shown) to define one sided limits:

• the left-hand limit (−) is 3.8
• the right-hand limit (+) is 1.3

And the ordinary limit 'does not exist'

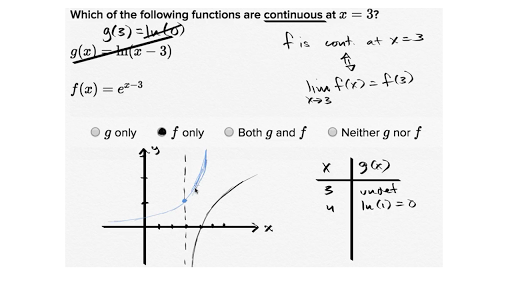
Are limits only for difficult functions?

Limits can be used even when we know the value when we get there! Nobody said they are only for difficult functions.

Example:

limx→10x2 = 5

10 x/2 = 5 -->

We know perfectly well that 10/2 = 5, but limits can still be used (if we want!)

Approaching Infinity

Infinity is a very special idea. We know we can't reach it, but we can still try to work out the value of functions that have infinity in them.

Let's start with an interesting example.

Question: What is the value of 1∞ ?

1 Limits & Continuityap Calculus Calculator

Answer: We don't know!

Why Don't We Know?

The simplest reason is that Infinity is not a number, it is an idea.

So 1∞ is a bit like saying 1beauty or 1tall.

Maybe we could say that 1∞= 0, ... but that is a problem too, because if we divide 1 into infinite pieces and they end up 0 each, what happened to the 1?

In fact 1∞ is known to be undefined.

But We Can Approach It!

So instead of trying to work it out for infinity (because we can't get a sensible answer), let's try larger and larger values of x:

x	1x
1	1.00000
2	0.50000
4	0.25000
10	0.10000
100	0.01000
1,000	0.00100
10,000	0.00010

Now we can see that as x gets larger, 1x tends towards 0

We are now faced with an interesting situation:

• We can't say what happens when x gets to infinity
• But we can see that 1x is going towards 0

We want to give the answer '0' but can't, so instead mathematicians say exactly what is going on by using the special word 'limit'.

The limit of 1x as x approaches Infinity is 0

And write it like this:

limx→∞1x = 0

INF 1/x = 0 -->

In other words:

As x approaches infinity, then 1x approaches 0

It is a mathematical way of saying 'we are not talking about when x=∞, but we know as x gets bigger, the answer gets closer and closer to 0'.

Read more at Limits to Infinity.

Solving!

We have been a little lazy so far, and just said that a limit equals some value because it looked like it was going to.

That is not really good enough! Read more at Evaluating Limits.

OSHA recognizes that many of its permissible exposure limits (PELs) are outdated and inadequate for ensuring protection of worker health. Most of OSHA’s PELs were issued shortly after adoption of the Occupational Safety and Health (OSH) Act in 1970, and have not been updated since that time. Section 6(a) of the OSH Act granted the Agency the authority to adopt existing Federal standards or national consensus standards as enforceable OSHA standards. Most of the PELs contained in the Z-Tables of 29 CFR 1910.1000 were adopted from the Walsh-Healy Public Contracts Act as existing Federal standards for general industry. These in turn had been adopted from the 1968 Threshold Limit Values (TLVs^®) of the American Conference of Governmental Industrial Hygienists (ACGIH^®). Some consensus standards from the American Standards Association were also adopted at that time, following the 6(a) procedures. Comparable PELs were adopted for shipyards (29 CFR 1915.1000) and construction (29 CFR 1926.55).

Since 1970, OSHA promulgated complete 6(b) standards including new PELs for 16 agents, and standards without PELs for 13 carcinogens.

1 Limits & Continuityap Calculus Ab

Industrial experience, new developments in technology, and scientific data clearly indicate that in many instances these adopted limits are not sufficiently protective of worker health. This has been demonstrated by the reduction in allowable exposure limits recommended by many technical, professional, industrial, and government organizations, both inside and outside the United States. Many large industrial organizations have felt obligated to supplement the existing OSHA PELs with their own internal corporate guidelines. OSHA’s Hazard Communication standard (1910. 1200 Appendix D) requires that safety data sheets list not only the relevant OSHA PEL but also the ACGIH^® TLV^® and any other exposure limit used or recommended by the chemical manufacturer, importer, or employer preparing the safety data sheet.

To provide employers, workers, and other interested parties with a list of alternate occupational exposure limits that may serve to better protect workers, OSHA has annotated the existing Z-Tables with other selected occupational exposure limits. OSHA has chosen to present a side-by-side table with the Cal/OSHA PELs, the NIOSH Recommended Exposure Limits (RELs) and the ACGIH^® TLVs^®s. The tables list air concentration limits, but do not include notations for skin absorption or sensitization.

OSHA’s mandatory PELs in the Z-Tables remain in effect. However, OSHA recommends that employers consider using the alternative occupational exposure limits because the Agency believes that exposures above some of these alternative occupational exposure limits may be hazardous to workers, even when the exposure levels are in compliance with the relevant PELs.

• California Division of Occupational Safety and Health (Cal/OSHA) Permissible Exposure Limits (PELs).

  Cal/OSHA has established an extensive list of PELs (Cal/OSHA AC-1 Table) that are enforced in workplaces under its jurisdiction. Cal/OSHA PELs are promulgated under statutory requirements for risk and feasibility that are no less protective than the OSH Act. Though not enforceable in establishments outside of Cal/OSHA’s jurisdiction, the PELs can provide information on acceptable levels of chemicals in the workplace. Of all the states that have OSHA-approved State Plans, California has the most extensive list of OELs.

• National Institute for Occupational Safety and Health (NIOSH) Recommended Exposure Limits (RELs).

  NIOSH RELs are authoritative Federal agency recommendations established according to the legislative mandate for NIOSH to recommend standards to OSHA. RELs are intended to limit exposure to hazardous substances in workplace air to protect worker health. In developing RELs and other recommendations to protect worker health, NIOSH evaluates all available medical, biological, engineering, chemical, and trade information relevant to the hazard. NIOSH transmits its recommendations to OSHA for use in developing legally enforceable standards. NIOSH also publishes its recommendations in publicly available sources such as the NIOSH Pocket Guide to Chemical Hazards, Criteria Documents, Current Intelligence Bulletins, Alerts, Special Hazard Reviews, Occupational Hazard Assessments, and Technical Guidelines.

• ACGIH^® Threshold Limit Values (TLVs^®) and Biological Exposure Indices (BEIs^®).

  ACGIH^® is a private, not-for-profit, nongovernmental corporation. It is not a standards setting body. ACGIH^® is a scientific association that develops recommendations or guidelines to assist in the control of occupational health hazards. TLVs^® and BEIs^® are health-based values and are not intended to be used as legal standards.

  Threshold Limit Values (TLVs^®) refer to airborne concentrations of chemical substances and represent conditions under which it is believed that nearly all workers may be repeatedly exposed, day after day, over a working lifetime, without adverse effects.

  Biological Exposure Indices (BEIs^®) are guidance values for assessing biological monitoring results – concentrations of chemicals in biological media (e.g., blood, urine). BEIs^® represent the levels of determinants that are most likely to be observed in specimens collected from healthy workers who have been exposed to chemicals in the same extent as workers with inhalation exposure at the TLV^®.

  Since ACGIH^® TLVs^® and BEIs^® are based solely on health factors, there is no consideration given to economic or technical feasibility. ACGIH^® does not believe that TLVs^® and BEIs^® should be adopted as standards without an analysis of other factors necessary to make appropriate risk management decisions (e.g., control options, technical and economic factors, etc.).

  For more information on TLVs^®, please go to https://www.acgih.org/TLV/. The TLVs^® and BEIs^® are copyrighted by ACGIH^® and are not publicly available. However, they can be purchased in their entirety on the ACGIH^® website at https://www.acgih.org/store/. Permission must be requested from ACGIH^® to reproduce the TLVs^® and BEIs^®. Click here for permission request form.

  The ACGIH^® TLVs^® are widely recognized as authoritative, and are required to be included on safety data sheets by the OSHA Hazard Communication Standard.

Annotated PELs Tables

OSHA’s annotated PELs tables include a side-by-side comparison of OSHA PELs, Cal/OSHA PELs, NIOSH RELs and ACGIH^® TLVs^®. The TLVs^® in the annotated tables are reprinted with permission from ACGIH^®. See Important Note on ACGIH^® TLVs^®, which is also reprinted with permission from ACGIH^®. Cal/OSHA, NIOSH, and ACGIH have OELs in addition to those listed in the annotated tables. The annotated tables contain links to the complete OEL lists from Cal/OSHA and NIOSH. TLVs^® and BEI^®s are not publicly available, but can be purchased on ACGIH^®'s website. For the most current OELs and information on notations such as skin absorption, users should consult complete listings and explanations from Cal/OSHA, NIOSH, and ACGIH.

1 Limits & Continuityap Calculus 14th Edition

Each of the alternative lists of exposure limits is accompanied by extensive explanatory language on their source websites. These include averaging periods, size selective measures and similar information. In particular, ACGIH^® provides an explanation of the use of TLVs^® and access to documentation. For more information and documentation, consult with these organizations.